Ha llegado el equinoccio.

Ha llegado el otoño.
Y el sol cada día sale más tarde y se pone antes. El día decrece y la noche crece.

El primer día del otoño ha sido el 22 de septiembre. Es el equinoccio ("igual noche"). Justo ese día en que la noche es igual de larga que el día.

Pero en realidad es hoy, día 25, cuando vemos 12 horas de sol y 12 horas sin sol.

En esta página de meteogram.es obtenemos la horas de salida y puesta del Sol y la duración del día en Castro Urdiales:

Día	Horas de luz
22 de septiembre	12 h   9 min	←equinoccio
23 de septiembre	12 h   6 min
24 de septiembre	12 h   3 min
25 de septiembre	12 h	←equilux

Pero, ¿no decíamos que "día = noche"? ¿Por qué 9 minutos más de luz en el equinoccio?

Uno:
Porque el borde del sol sale antes que su centro y porque el borde del sol se mete después que su centro.
Es decir: por ser un "disco", vemos el Sol más tiempo que si sólo fuera un puntito en el cielo.
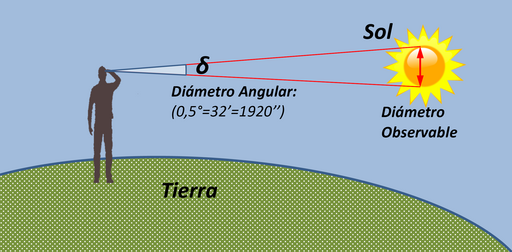
El diámetro del sol es de 32' (minutos de grado).

Por tanto:
- al amanecer, el borde del Sol aparece 16' por delante de su centro, y
- al anochecer, el borde del Sol desaparece 16' por detrás de su centro.

Imagen de Luis Algerich (c) encontrada en enepod.usra.edu

Dos:
Porque los rayos del sol se refractan (se curvan) en la atmósfera y vemos el sol más alto de lo que en realidad está.
En la salida del Sol lo vemos 34' antes de que suba por encima del horizonte,
y en la puesta del Sol lo vemos 34' después de que baje por debajo del horizonte.

Tres:
Porque la Tierra no es plana sino casi esférica, lo que hace que el horizonte aparente esté 3' por debajo del horizonte plano.

En total, vemos el Sol durante un ángulo adicional de  16' +34' +3' al amanecer, y lo mismo al anochecer. En total, 106'.
¿Cuánto tiempo es esto?  Regla de tres:

   360° (una vuelta) son recorridos en    24 horas
        106'                          son recorridos en      x minutos

Por tanto:  x = 106'·24h/360°  = 106'·24·60min/(360·60') = 7,1 minutos de tiempo.


Pero en la tabla pone 12h 9min. ¿A qué se debe la diferencia desde 7 minutos hasta 9 minutos?
A que, cada día, el día disminuye 3 minutos. Por tanto, hay 3 minutos de diferencia entre el posible caso de equinoccio a las 00:01 horas y el posible caso de equinoccio a las 23:59 horas. Depende de la hora a la que ocurra el equinoccio.

Equinoccio de otoño	Horas de luz
año 2020	12 h   9 min
año 2019	12 h   8 min
año 2018	12 h   8 min

Conclusión:    El día 22 vimos el Sol durante 12 horas y 9 minutos, pero en realidad el centro del Sol pasó 12 horas por debajo del horizonte plano y otras 12 horas por encima.

Concurso de fotografía matemática.

Puedes ver las bases del concurso en este enlace. Explican cómo tienen que ser las fotos y cómo puedes participar.

Y si quieres ver las fotos finalistas y ganadoras del curso pasado, mira la entrada de mayo de 2019 de este mismo blog.

¿Serás capaz de encontrar matemáticas cerca de tí?

Feliz año bisiesto.

¿Sabes por qué este año es bisiesto?

Pues porque la naturaleza no es tan exacta como nos gustaría.

Por ejemplo, en un año no caben exactamente 365 días, sino 365 y pico.
Más concretamente, en un "año solar" caben 365'2421904... "días solares".
(Para más detalles, mira la nota final).

Por eso, un calendario de 365 días no es exacto y necesita añadir un día más algunos años ("años bisiestos").

¿Pero cuándo un año debería ser bisiesto?
Hagamos varias aproximaciones:

Un año ~365 días	= 365
Un año ~365'25 días	= 365 + 0'25
	= 365 + 1/4
Un año ~365'24 días	= 365 + 0'25 - 0'01
	= 365 + 1/4 - 1/100
Un año ~365'2425 días	= 365 + 0'25 - 0'01+ 0'0025
	= 365 + 1/4 - 1/100 + 1/400

Nuestro calendario (llamado "calendario gregoriano" porque lo decretó el papa Gregorio XIII mediante una bula en 1582) sigue esta última aproximación.
Es decir: a los 365 días hay que:

añadir 1 día cada 4 años,
quitar 1 día cada 100 años
y añadir 1 día cada 400 años.

La regla es:

Un año es bisiesto si es divisible entre 4,
a menos que sea divisible entre 100.
Pero si es divisible entre 400, también es bisiesto.

¿Sabríamos mejorarlo? Claro:

Un año ~365'2422 días	= 365 + 0'25 - 0'01+ 0'0025 - 0'0003
	= 365 + 1/4 - 1/100 + 1/400 - 3/10000
	~ 365 + 1/4 - 1/100 + 1/400 - 1/3333

Como vemos, tendríamos que quitar 1 día cada 3333 años.
Sólo habría que decretar que los años 3333, 6666, etc. fuesen años de 364 días. ¿Antibisiestos?

Nota para saber más:

Un "día solar" es el tiempo entre el momento en que el sol está más alto un día y el momento en que pasa lo mismo al día siguiente.  Aunque cambia un poco a lo largo del año, en promedio ("día solar medio") son 86400 segundos.

Un "año solar" es más complicado de explicar:
La Tierra se mueve alrededor del Sol trazando una elipse plana (traslación). También gira en torno a sí misma (rotación), lo que define una línea llamada ecuador que separa el hemisferio norte del hemisferio sur.
Si el eje de rotación no estuviera inclinado más de 23 grados, el plano que pasa por el ecuador coincidiría con el plano de la traslación. Pero como está inclinado, el plano que pasa por el ecuador está inclinado con respecto al plano de la traslación, como las dos hojas de un libro entreabierto.
Por tanto, ambos planos se cortan en una línea recta llamada línea de los equinoccios. El Sol pasa por esta línea dos veces cada año: una cuando comienza el otoño (equinoccio de otoño: el Sol pasa de nuestro hemisferio Norte al hemisferio Sur) y otra cuando comienza la primavera (equinoccio de primavera: el Sol vuelve del Sur al Norte).
Un año solar es el tiempo que pasa desde que el Sol pasa por uno de estos puntos hasta que vuelve a pasar por él.

Imagen de wikimedia.org (dominio público)

Cada voto cuenta

Acabamos de pasar por unas elecciones al Congreso que convierten los votos en diputados. ¿Pero cómo se hace? La respuesta es el método de D'Hondt.

Ejemplo: Cantabria.

En Cantabria se reparten cinco diputados.  Para ello, se construye la siguiente tabla y se toman primero los números mayores:

	Votos	Votos/2	Votos/3	...
PP	84032	42016	28010	...
	Primero	Quinto
PSOE	75430	37715	25143	...
	Segundo	(Sexto)
PRC	68580	34290	22860	...
	Tercero	(Séptimo)
VOX	48600	24300	16200	...
	Cuarto
UP	28075	14037	9358	...
	(Octavo)
...	...	...	...	...

¿Y si se hubieran repartido ocho diputados?  Pues el 8º sería para UP. Y el PP se quedaría sin él por la pequeña diferencia de 65 votos.

Y es que cada voto cuenta.

ENTREGA DE PREMIOS DEL CONCURSO DE FOTOGRAFÍA MATEMÁTICA

El jueves 16 de mayo tuvo lugar la entrega de premios del concurso de fotografía matemática a la que asistieron los finalistas de cada categoría y otros alumnos acompañantes. Si te lo perdiste, ¡puedes revivirlo aquí!

I Gymkhana Matemática de Cantabria

El viernes 3 de mayo cuatro equipos de 4 alumnos de nuestro instituto participaron en la I Gymkhana Matemática de Cantabria organizada por el departamento de matemáticas del IES Valle de Piélagos y en la que colaboraron profesores de distintos centros incluido el IES Dr. José Zapatero Domínguez. La Gymkhana, que estaba dirigida al alumnado de 3ºESO y en la que participaron cerca de 170 alumnos de centros de nuestra región, constaba de 7 estaciones en las que había una prueba relacionada con la lógica, el ingenio y el razonamiento matemático.

ALUMNOS DE 4º ESO RETAN A CIENTÍFICOS EN UN CONCURSO A TRAVÉS DE INTERNET

Algunos de los alumnos de 4ºESO han estado interactuando con científicos de toda España en una actividad de divulgación a través de Internet cuyo objetivo es aumentar su interés por la ciencia.

En Somos Científicos, ¡sácanos de aquí!, estudiantes de 10 a 18 años retan a investigadores en chats en los que pueden preguntar a especialistas sobre lo que quieran: desde tratamientos contra el cáncer, hasta cómo frenar el cambio climático, o cómo estudiar las estrellas más lejanas. En nuestro caso, quedamos encuadrados dentro de la Zona CSIC, por lo que pudimos interactuar con investigadores de distintos centros de este Consejo.